地震偏移
地震偏移是将地震事件在空间或时间上几何重新定位到事件在地下发生的位置而不是在地面记录的位置的过程,从而创建更准确的地下图像。这个过程对于克服复杂地质区域所施加的地球物理方法的局限性是必要的,例如:断层、盐体、褶皱等。[1] [2] [3]
偏移将倾角反射器移动到它们真正的地下位置并折叠衍射,[4]导致偏移图像通常具有更高的空间分辨率,并且比非偏移图像更好地解析复杂地质区域。一种偏移形式是基于反射的地球物理方法(地震反射和探地雷达) 的标准数据处理技术之一
自从地震勘探开始以来,人们就了解了偏移的必要性,并且迁移了 1921 年的第一批地震反射数据。[5]计算迁移算法已经存在多年,但它们只是在过去 20 年才开始广泛使用,因为它们非常耗费资源。迁移可以导致图像质量的显着提升,因此算法是地球物理行业和学术界深入研究的主题。
基本原理[编辑]
图表显示了来自水平反射器的零偏移反射的射线路径。
图表显示了倾角反射器的零偏移反射的射线路径和由此产生的表观倾角。
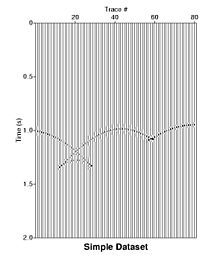
零偏移量非迁移数据集。恒速世界中简单向斜的原始零偏移距数据。请注意图像中标志性的领结效果。这是从向斜两侧发生反射并在不同时间到达同一接收器的结果。迁移可以纠正这种影响。
File :SimpleSyncline.jpg数据的零偏移迁移数据集。该数据是使用称为相移的时间偏移进行迁移的,该时间偏移在傅立叶域中运行。迁移已将所有事件替换到正确位置,成功重建向斜。然而,整个图像中存在由迁移引起的噪声的错误事件(摆动弧)。
地震波是一种弹性波,它以有限的速度在地球中传播,受地震波所在岩石的弹性特性控制。在具有不同声阻抗的两种岩石类型之间的界面处,地震能量要么被折射,要么被反射回表面,要么被介质衰减。反射能量到达地表并由放置在距波源已知距离处的地震检波器记录。当地球物理学家查看地震检波器记录的能量,他们知道传播时间和源与接收器之间的距离,但不知道到反射器的距离。
在最简单的地质环境中,具有单个水平反射器、恒定速度和同一位置的源和接收器(称为零偏移,其中偏移是源和接收器之间的距离),地球物理学家可以确定位置通过使用关系的反射事件:
其中 d 是距离,v 是地震速度(或传播速度),t 是从震源到接收器的测量时间。
在这种情况下,距离减半,因为可以假设从源到达反射器只需要总传播时间的一半,然后另一半返回接收器。
结果给了我们一个单一的标量值,它实际上代表距离源/接收器的半个球体,反射可能起源于此。它是一个半球体,而不是一个完整的球体,因为我们可以忽略所有发生在表面之上的不合理的可能性。在水平反射器的简单情况下,可以假设反射垂直位于源/接收器点下方(见图)。
在倾角反射器的情况下,情况更为复杂,因为第一次反射起源于倾角方向的更上方(见图),因此旅行时间图将显示减少的倾角,这定义了“迁移器方程”:[5]
其中ξ a是视倾角,而ξ是真实倾角。
零偏移距数据对地球物理学家很重要,因为偏移操作要简单得多,并且可以用球面表示。当以非零偏移获取数据时,球体变成椭圆体并且表示起来要复杂得多(无论是在几何上还是在计算上)。
使用[编辑]
对于地球物理学家来说,复杂地质学被定义为在横向和/或垂直速度方面存在突然或鲜明对比的任何地方(例如,岩石类型或岩性的突然变化导致地震波速度的急剧变化)。
地球物理学家认为复杂地质的一些例子是:断层、褶皱、(一些)压裂、盐体和不整合面。在这些情况下,使用一种称为叠前偏移 (PreSM) 的偏移形式,其中在移动到零偏移之前偏移所有轨迹。因此,使用了更多的信息,从而产生了更好的图像,以及 PreSM 比叠后偏移更准确地接受速度变化的事实。
迁移类型[编辑]
根据预算、时间限制和地下地质情况,地球物理学家可以采用两种基本类型的偏移算法中的一种,由它们的应用领域定义:时间偏移和深度偏移。
时间迁移[编辑]
时间偏移应用于时间坐标中的地震数据。这种类型的迁移假设只有轻微的横向速度变化,并且在存在最有趣和复杂的地下结构(尤其是盐)时会失效。一些常用的时间偏移算法是:Stolt 偏移,[6] Gazdag [7]和有限差分偏移。
深度偏移[编辑]
深度偏移应用于深度(正笛卡尔)坐标中的地震数据,深度坐标必须根据时间坐标中的地震数据进行计算。因此,该方法确实需要速度模型,这使其成为资源密集型,因为建立地震速度模型是一个漫长而反复的过程。这种偏移方法的显着优点是它可以成功地用于具有横向速度变化的区域,这些区域往往是石油地质学家最感兴趣的区域。一些常用的深度偏移算法是基尔霍夫深度偏移、逆时偏移 (RTM)、[8]高斯波束偏移[9]和波动方程偏移。[10]
分辨率[编辑]
偏移的目标是最终提高空间分辨率,并且对地震数据所做的基本假设之一是它仅显示初级反射并且已去除所有噪声。[5] 为了确保最大分辨率(从而最大程度地提高图像质量),应在迁移前对数据进行充分预处理。在迁移过程中,可能很容易区分预迁移的噪声可能会在整个孔径长度上涂抹,从而降低图像的锐度和清晰度。
进一步的基本考虑是使用 2D 还是 3D 偏移。如果地震数据具有交叉倾角元素(垂直于采集线倾角的层),则主反射将源自面外,而 2D 偏移无法将能量放回原点。在这种情况下,需要进行 3D 偏移以获得最佳图像。
现代地震处理计算机进行 3D 偏移的能力更强,因此是否分配资源来执行 3D 偏移的问题不再受到关注。
图形迁移[编辑]
一个简单的图形迁移的例子。在 1960 年代和 70 年代现代计算机出现之前,这是地球物理学家用于原始“迁移”数据的一种方法。随着数字处理器的出现,这种方法已经过时,但对于理解迁移背后的基本原理很有用。
最简单的迁移形式是图形迁移。图形偏移假设一个恒定速度的世界和零偏移数据,其中地球物理学家绘制从接收器到所有事件的事件位置的球体或圆圈。圆圈的交点形成了反射器在时间或空间上的“真实”位置。图中可以看到这样的一个例子。
技术细节[编辑]
 |
本节**未引用任何来源*。请通过添加对可靠来源的引用来帮助改进此部分。无来源的材料可能会受到质疑和删除。 *(2015 年 10 月)**(了解如何以及何时删除此模板消息) |
|---|---|
地震数据偏移是通过地震数据的基于网格的数值空间卷积来修正平坦地质层假设,以解释倾斜事件(地质层不平坦)。有很多方法,例如流行的基尔霍夫偏移,但人们普遍认为,一次处理数据的大空间部分(孔径)引入的错误更少,并且深度偏移远优于具有大倾角和复杂的盐体。
基本上,它将能量(地震数据)从记录的位置重新定位/移动到具有正确公共中点 (CMP) 的位置。虽然地震数据最初是在适当的位置接收到的(根据自然法则),但这些位置与该位置的假设 CMP 并不对应。尽管在没有偏移校正的情况下叠加数据会产生不太准确的地下图片,但迁移是首选,因为大多数成像记录仪可以更好地钻探和维护油田。此过程是从活动源创建地下图像的核心步骤在地表、海床、钻孔等处收集的地震数据,因此被石油和天然气公司及其服务提供商在数字计算机上以工业规模使用。
换句话说,这个过程试图解释倾角反射器的波分散以及空间和方向地震波速度(异质性)变化,这导致波场(由射线路径建模)弯曲,波前交叉(焦散) , 并且在与直线或其他简化假设下预期的位置不同的位置记录波。最后,这个过程通常还试图保存和提取嵌入在地震数据振幅中的地层界面反射率信息,以便它们可用于重建地质构造的弹性特性(振幅保存、地震反演). 偏移算法有很多种,按其输出域可分为时间偏移或深度偏移、叠前偏移或叠后偏移(正交)技术等大类。深度偏移始于通过空间地质速度剖面将时间数据转换为深度数据。叠后偏移从已经叠加的地震数据开始,因此已经丢失了有价值的速度分析信息。
考虑图 4.1-1a 中简单地质剖面的倾角反射体CD 。我们想要获得沿剖面Ox 的零偏移距部分。当我们沿Ox移动源-接收器对 ( s, g )时,来自倾角反射器的第一个法向入射到达被记录在位置A处。在本次讨论中,我们假设归一化恒速介质v = 1,以便时间和深度坐标可以互换。在图 4.1-1b 中零偏移距时间段上的C’点表示位置A的反射到达。当我们从位置A移动时在右侧,垂直入射到达是从倾角反射器CD记录的。最后一次到达记录在位置B ,如图 4.1-1b 中的点**D’所示。在这个实验中,排除了反射器CD边缘的衍射以简化讨论。
将图 4.1-1a 中的地质剖面(深度)与图 4.1-1b 中的零偏移距地震剖面(时间)进行比较。反射器CD的真实地下位置叠加到时间截面上以进行比较。显然反射体CD的真实地质位置与反射事件位置*C’D’*并不相同。
从这个简单的几何构造中,请注意时间段C’D’中的反射必须迁移到其在深度段中的真实地下位置CD 。从图 4.1-1 中 迁移的几何描述可以得出以下观察结果:
图 4.0-1 中的示例演示了上述观察结果。特别地,倾角事件 ( B ) 已经向上倾方向移动,变短,并且在偏移( A ) 之后变得陡峭。
上一节讲到,常规的迁移输出是及时显示的,输入的stacked section也是如此。为了区分两个时间轴,我们将堆叠截面上的时间轴表示为t — 未迁移位置的事件时间,迁移截面上的时间轴表示为τ — 迁移位置的事件时间。
我们现在将检查偏移时间部分上看到的水平和垂直位移。从图 4.1-2 中,考虑反射器段CD。假设CD迁移到C’D’并且**C’D’上的点E ‘迁移到**CD上的点E。水平和垂直(时间)位移 — d x和d t,以及倾角 Δ τ /Δ x,都是在偏移时间剖面上测量的(图 4.1-2),可以用介质速度v、走时t表示, 和表观倾角 Δ t/Δ x在未迁移时间段上测量(图 4.1-2)。Chun 和 Jacewitz [1]推导出以下公式:
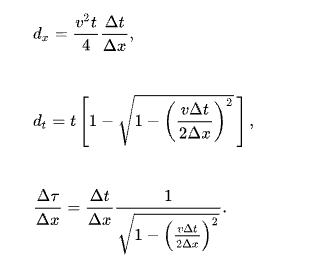
为了定量地了解这些表达式,我们考虑一个数值示例。对于随深度增加的真实速度函数,考虑不同深度的五个反射段。为简单起见,假设量 Δ t /Δ x对于所有的都是相同的(每 25 米迹线间距 10 毫秒)。根据等式 ( 1 )、( 2 ) 和 ( 3 ),计算迁移后的水平和垂直位移dx和dt以及倾角(单位为 ms/ trace )。结果总结在表 4-2 中。
参考表 4-2 和等式(**1)、(2)和(3**),并做出以下观察:
- 迁移部分的时间倾角 Δ τ /Δ x总是大于未偏移部分的时间倾角 Δ t /Δ x 。
- 在未迁移位置,水平位移d x随着事件时间t的增加而增加。4 s 时,水平位移超过 6 km。
- 水平位移d x是速度平方的函数。如果在迁移中使用的速度有 20% 的误差,那么该事件会因 44% 的误差而错位。
- 垂直位移d t也随着时间和速度而增加。
- 事件倾角越陡,偏移后的水平和垂直位移越大。
| 吨(秒) | v(米/秒) | 深×(米) | d t (s) | Δt / Δx (毫秒/迹线) | Δτ / Δx (毫秒/迹线) |
|---|---|---|---|---|---|
| 1个 | 2500 | 625 | 0.134 | 10 | 11.5 |
| 2个 | 3000 | 1800 | 0.400 | 10 | 12.5 |
| 3个 | 3500 | 3675 | 0.858 | 10 | 14.0 |
| 4个 | 4000 | 6400 | 1.600 | 10 | 16.7 |
| 5个 | 4500 | 10125 | 2.820 | 10 | 23.0 |
在图 4.1-1a 中,假设仅在表面位置A和B之间记录了零偏移距剖面。时间部分将包含事件C’D’,但在迁移时,事件将迁移出该部分,从而导致迁移部分为空白(图 4.1-1b)。因此,叠加剖面上的数据不一定局限于地震测线以下的地下。反过来更重要;地震线以下的构造可以不记录在地震剖面上。假设数据仅记录在地表位置O和A之间。这一次,生成的时间部分将是空白的。所以,我们不应该在A和B之间记录,我们也不应该在O和A之间记录。相反,我们应该在O和B之间记录,以便正确记录感兴趣的反射器并正确迁移它。
在具有结构倾角的区域,必须通过考虑倾角事件相对于引起事件的结构的水平位移来选择线长。这是一个重要的考虑因素,尤其是在 3-D 地震工作中。调查的区域表面覆盖范围通常大于感兴趣的区域地下覆盖范围。
要获得完整的倾角反射镜图像,记录时间也必须足够长。例如,如果仅记录OE秒(图 4.1-1),则记录的片段**C′D″将仅产生完整图像CD的一部分。图 4.0-1 显示了一个记录更深时间和更长线长度以实现更陡倾角的极好示例。盐丘边界的正确成像需要记录超过 6 秒的数据。
-
图4.1-1 偏移原理: (b)时间段内的反射段C′D′偏移时向上倾斜、变陡、变短,映射到(a)的真实地下位置CD 。改编自[1]。
-
图 4.0-1 CMP 堆栈 (a) 迁移前,(b)迁移后;(c) 在 (B)迁移之前和之后 (A) 迁移的显着衍射 D 和倾斜事件的草图。迁移将倾斜事件 B 移动到其假定的真实地下位置 A,并将衍射 D 折叠到其顶点 P。虚线表示盐丘的边界。
-
图 4.1-2迁移过程 的定量分析。未偏移部分(左)上的倾斜事件AB移动到偏移部分(右)上的A’B’ 。迁移后的事件也叠加在未迁移的部分上,以比较迁移前后事件的位置。偏移后倾角反射镜AB上的**C点移动到C’。水平位移量d x、垂直位移量d t和倾角 Δ τ /Δ x之后迁移由等式 ( 1 )、( 2 ) 和 ( 3 )计算得出。
图 4.1-3中的浸没事件模型进一步说明了上述迁移概念。这里包括边缘衍射。由于偏移,零偏移距剖面上的倾角反射体变陡、变短并向上倾方向移动。图 4.1-4 显示了偏移前后叠置剖面上一系列倾斜事件的现场数据示例。请注意,倾角越陡,迁移后事件移动得越多。
到目前为止,只考虑了线性反射器。我们现在考虑涉及弯曲反射界面的更现实的地质情况。图 4.1-5 显示了三个向斜和一个小的背斜特征。向斜在零偏移距部分显示为蝴蝶结。通过使用从图 4.1-1 的几何推导出的原理,请注意由于偏移,领结的A段在向上倾斜的方向上向左移动。类似地,B段向右移动,而平顶段C根本没有移动太多。因此,迁移后与向斜相关的领结侧翼被打开。另一方面,小背斜在零偏移距剖面上似乎比在偏移剖面上更宽。再次注意,由于迁移,D段向右上倾移动,而E段向左上倾移动。因此,由于迁移,向斜变宽而背斜变窄。迁移速度也会影响结构的外观尺寸;更高的速度意味着更多的迁移,因此意味着更小的背斜结构。
-
图 4.1-3 (a) 由 (b) 中所示的倾角反射器建模的零偏移剖面。介质速度恒定为 3500 m/s,迹线间距为 25 m。反射器的真实倾角在 0 到 45 度之间以 5 度为增量变化。零偏移距部分 (a) 的偏移产生倾角反射器 (b) 的模型。
-
图 4.1-4 CMP 堆栈的一部分(a)迁移前和(b)迁移后。请注意具有从断层平面散开的一系列倾角的事件组。迁移使它们向上倾斜,使它们更短、更陡峭。
-
图4.1-5 弯曲反射界面(向斜和背斜)(a)迁移前和(b)迁移后。详情见正文。(模型由 Union Oil Company 提供。)
-
图 4.1-6 (a) 由向斜反射层组成的速度-深度模型;(b) 在零偏移距部分选择的正常入射到达。在时间部分跟踪领结。
为什么向斜在堆积截面上看起来像领结?答案在图 4.1-6 中,其中模拟了对称向斜。给定图 4.1-6a 中的地下模型,可以计算法向入射射线以导出图 4.1-6b 中的零偏移距走时剖面。为清楚起见,仅显示了五个 CMP 位置。在位置 2 和 4,有两个不同的到达,而在位置 3,有三个不同的到达。通过填充中间射线路径,可以在时间段上构造向斜的蝴蝶结特征。通过追踪图 4.1-6b 中的走时轨迹来完成该过程。
图 4.1-7 和 4.1-8 显示了两个包含向斜和背斜构造的野外数据示例。在图 4.1-7 中,注意由于迁移,向斜特征变宽,背斜特征变窄。在图 4.1-8 中,与两个小向斜盆地A和B相关的蝴蝶结在深度上变大。迁移后,解开蝴蝶结,划定向斜。